Here are some of the research projects I have participated in over the years, please check out the publications page for the corresponding papers.

• Error correction for DNA storage
• FASTQ compression
• Time series data compression
• Multimedia compression for humans
• Other projects

• Error correction for DNA storage (Ph.D. research)
  Stanford University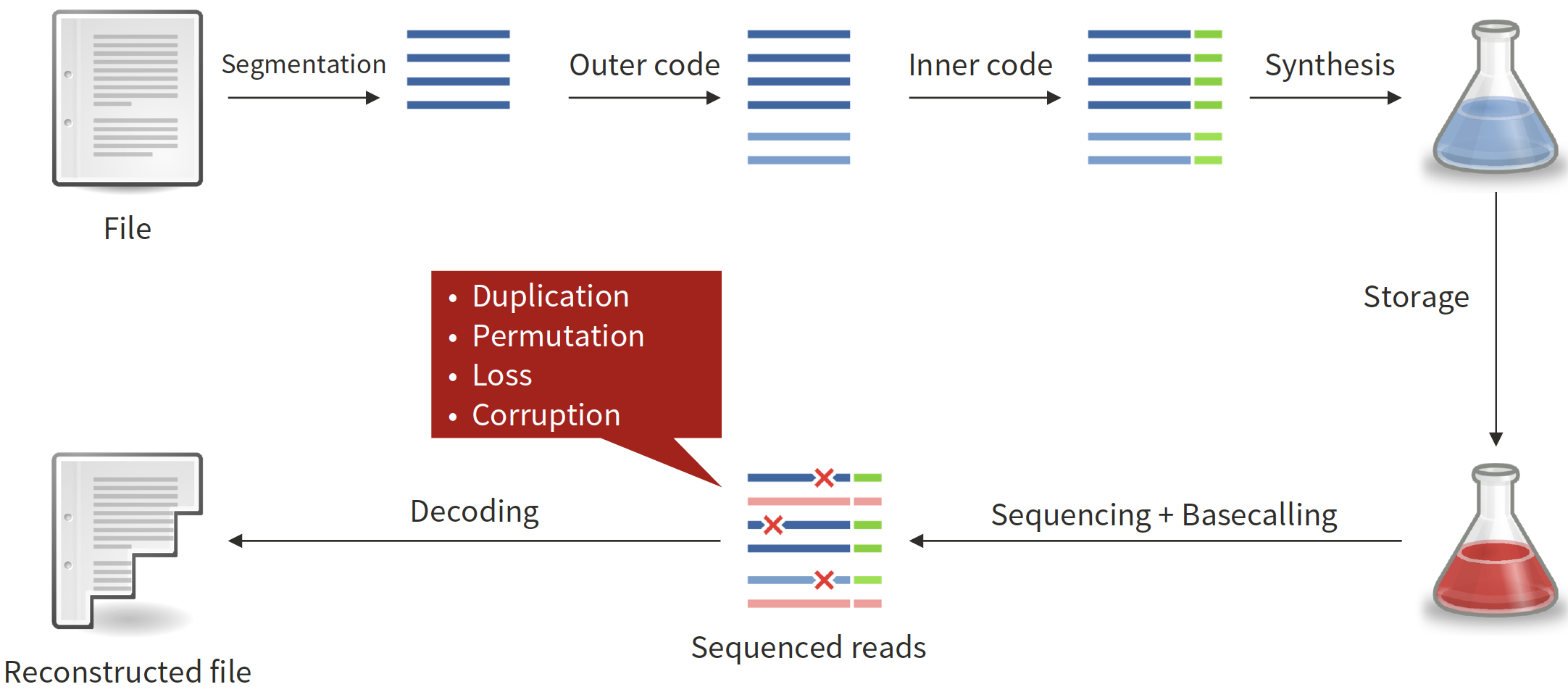

  

  Introduction: DNA as a storage medium can provide high storage density and long-term durability, and hence can be an alternative for traditional magnetic/semiconductor-based storage media in the near future. However, the DNA synthesis and sequencing processes are expensive and noisy, and there is a need to design optimized encoding/decoding schemes with error correction for reliable data recovery. In particular, nanopore sequencing provides low cost, portable and real-time solution at the expense of higher error rates making error correction coding critical.

  • We studied the tradeoff between the writing and reading costs involved in DNA-based storage and propose a practical scheme based on LDPC codes to achieve an improved tradeoff between these quantities.
  • For nanopore sequencing based DNA storage, we proposed a novel approach which overcomes the high error rates in nanopore sequencing by exploiting the soft information available in the raw signals.
  • Check out my talk at ISMB/ECCB 2019 to get a high-level overview of this work. Also check out the panel on DNA storage I moderated at the Stanford Compression Workshop 2021.

[Back to top]

• Genomic data compression (Ph.D. research)
  Stanford University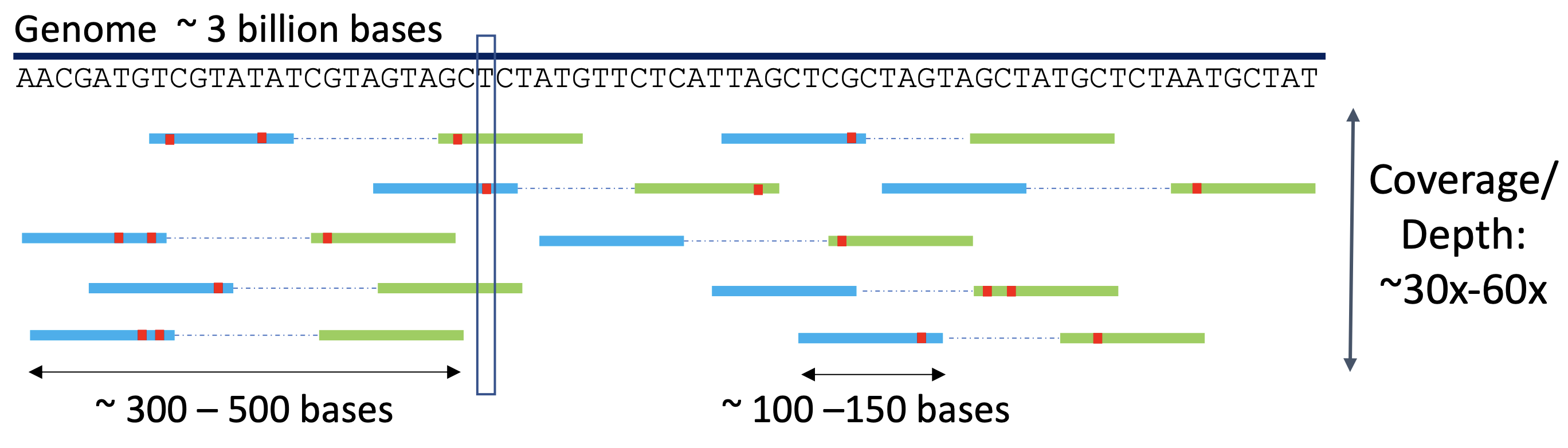

  

  Introduction: Next generation sequencing of genomes produces large amounts of data in the form of reads which are stored in FASTQ files. For a typical experiment, these files can be 100s of GBs large.

  • Performed theoretical analysis of the problem by computing upper bounds on the entropy of reads and developed HARC, a tool to compress reads with and without preserving their order, achieving near-optimal compression ratios.
  • Improved upon HARC to develop SPRING, a practical tool to compress single and paired-end FASTQ files, supporting a variety of modes and features.
  • Work published in Bioinformatics.
  • Check out my talk at ISMB/ECCB 2019 to get an overview of this work.
  • Integrated parts of SPRING with genie, an open-source MPEG-G codec.
  • Developed an algorithm to extend these ideas to long nanopore reads with higher error rates: NanoSpring. Also worked on methods to lossily compress raw signal files which are the precursors to nanopore FASTQ files.
  • Check out my PhD defense talk focused on my work on genomic data compression.

[Back to top]

• Time series data compression (Ph.D. research)
  Stanford University (in collaboration with Siemens)

  

  Time series data compression is increasing becoming critical with the large volumes of data produced by IoT devices and sensors. Lossy compression is often appropriate for such datasets due to the presence of noise and can lead to huge compression gains without sacrificing accuracy of downstream analysis.
  We developed LFZip, an error-bounded lossy compressor for multivariate floating-point time series data based on the prediction quantization-entropy coder framework. LFZip benefits from improved prediction using linear models and neural networks and outperforms the existing state-of-the-art error-bounded lossy compressors on several time series datasets. Check out my talk at DCC 2020 here.

[Back to top]

• Multimedia compression for humans (Ph.D. research)
  Stanford University

  Multimedia compression is crucial for today’s internet streaming traffic, and there is much interest in making the algorithms retain the most important aspects from the human perspective. With some great high school interns, we developed highly innovative methods to understand the limits of compression designed for humans.

  

  Studied image compression performed by humans for humans, by describing the image in terms of a text description [website].

  

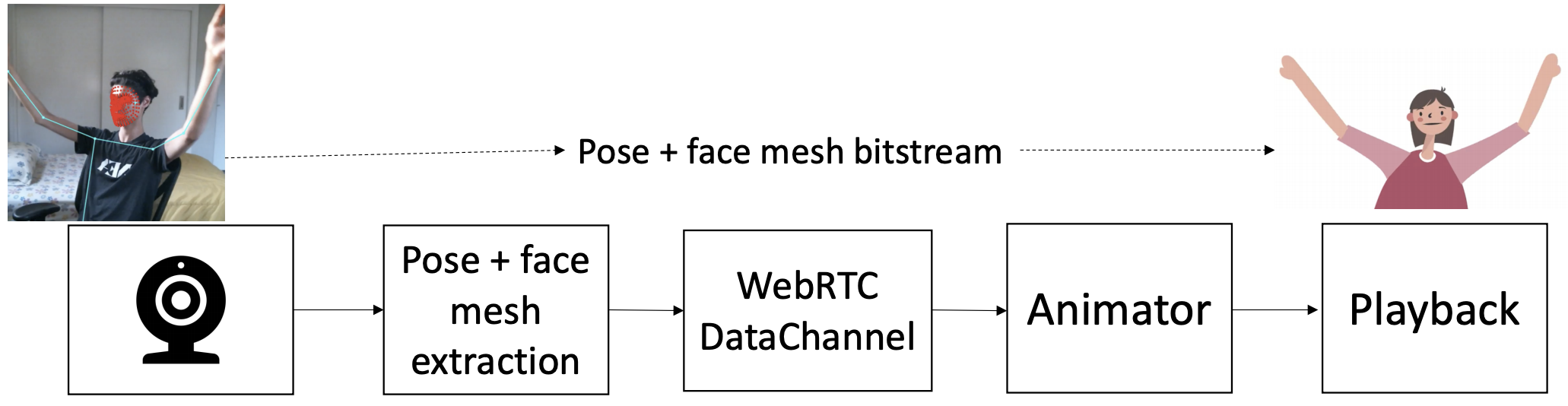
  Developed prototype video streaming pipeline that simply sends key points on the face leading to order-of-magnitude savings in bandwidth [website].

[Back to top]

• Applications of Gröbner Basis (B. Tech. Project)
  August 2015 - May 2016
  IIT Bombay
  Guide: Prof. Harish Pillai

  Introduction: Gröbner Basis is a computational tool for studying ideals in multivariate polynomial rings. It has applications in Commutative Algebra, Integer Optimization, Control Systems and other areas.

  • Studied the basic Gröbner basis theory and its connections to convex polytopes, toric ideals, integer programming and regular triangulations.
  • Obtained new relations for the pole placement problem using state feedback in single input systems by interpreting results from Gröbner bases in the control theoretic setting.
  • Extended the formulae to multi-input system using Gröbner basis and linear algebra.

  [report]

[Back to top]

• Elliptic Curve Cryptography for IoT (Summer internship)
  May 2015 - July 2015
  Massachusetts Institute of Technology
  Guide: Prof. Anantha Chandrakasan

  Introduction: Securing the Internet of Things is a major challenge due to the area and power constraints. Elliptic Curve Cryptography (ECC) is the most suitable public key scheme for IoT due to the small key sizes. Our aim was to design a ECC scalar multiplication processor for constrained applications.

  • Implemented Datagram Transport Layer Security (DTLS) handshake on low power ARM Cortex-M0+ processor using Arduino WiFiShield to identify the bottleneck operations during secure communication.
  • Surveyed existing low-area/energy implementations of ECC and studied Koblitz curves which have a Frobenius endomorphism allowing faster scalar multiplication using τ-adic representation.
  • Designed an integer to τ -adic converter which was absent from the existing low-area implementations, with only a marginal increase in area by reusing the registers and ALU.
  • Work published in IEEE Journal of Solid-State Circuits.

[Back to top]

• Functional Electrical Stimulation - Numerical Analysis (Summer internship)
  May 2014 - July 2014
  Oxford Brookes University, Oxford, UK
  Guides: Dr. Cristiana Sebu, Oxford Brookes University, UK; Dr. Brian Andrews, Nuffield Department of Surgical Sciences, University of Oxford, UK

  Introduction: Functional Electrical Stimulation (FES) is a technique that uses electric currents to activate nerves, helping restore function in people with disabilities. The challenge is to design electrodes which produce high nerve activation at desired depth while keeping surface current densities low.

  • Concentric Electrodes: Formulated Laplace equation for three-layer body model as integral equations using Hankel transform. The Nyström method with Gauss-Legendre quadrature was used to solve these equations. The Fourier-Bessel series was introduced to evaluate oscillatory integrals.
  • Non-concentric Electrodes: For square and other electrodes, a Finite Element model was solved using EIDORS software on MATLAB.
  • Compared various electrode configurations for safety and effectiveness using MATLAB simulations.

[Back to top]

• Spiking Neural Networks May 2013 - December 2013
  IIT Bombay
  Guide: Prof. Bipin Rajendran

  Introduction: Spiking Neural Networks (SNNs) can represent complex temporal relations between the input and output. Our aim was to study and implement algorithms for training of SNNs inspired by the brain.

  • Studied spiking neuron models as well as Artificial Neural Networks.
  • Studied and implemented ReSuMe, a supervised learning technique for SNNs based on Spike Timing Dependent Plasticity (STDP), on MATLAB.

[Back to top]